In the first place I would like to thank Simon Anthony (Cracking The Cryptic) and Bernhard Hobiger (HoDoKu), who inspired me to set up this website.

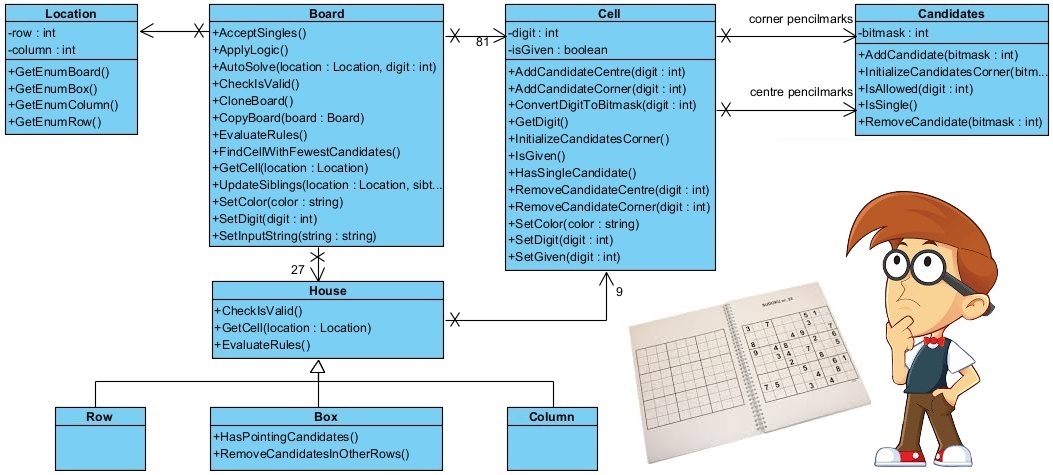
Simon Anthony often talks about the beauty of sudoku logic. This site is about the beauty of analysis-, design- and programming logic. The goal of this site is to inspire people to dive into the wonderful world of software development using modeling techniques like UML, the Unified Modeling Language.

So here UML is used to build up a sudoku webapp from scratch.You can find the resulting app and the source code under the Sudoku menu. On a desktop you can find the sourcecode under your browsers' menu as well . Examine how the app has been developed, examine the code, play sudoku and have fun!

Let's start the development process of the app with a basic use case outline,

Use case Solve sudoko:

  1. Load a hard sudoku puzzle
  2. Apply basic sudoku logic until the app gets stuck
  3. Apply advanced sudoku techniques to break the puzzle
  4. Check your solution

Wow, that's all you need to start with!

A use case describes functional requirements. It is always a good idea to start with a short clear outline of the "happy day" flow, the shortest way to reach the goal of the use case. Alternative "rainy day" flows can be postponed.

Each step can be refined, as shown below. 

Load sudoku puzzle

  • Copy and paste: Copy a standard sudoku string like ..1.....7...89..........6..26..3.......5...749...........1.4.5.83.............2.. from a website and paste it into the dropbox. Load and start the game by pressing the "Load" button.
  • Import file, using the "Import file" button
  • Manually: Clear the grid using the "Clear" button, enter the givens and load and start the game by using the "Load" button

Apply basic sudoku logic

Let the app apply these basic rules by pressing the "Apply logic" button. Note that 95% of  sudoku's from newspapers and magazines can be solved with applying only these 6 rules!

Apply advanced sudoku logic

Apply advances solving techniques like X-wings, Swordfishes, Y-wings, Almost Locked Sets, loops and so on, see http://hodoku.sourceforge.net/en/techniques.php. Switch between corner pencil marks (candidates for a row, column or box), centre pencil marks (candidates for a cell), normal (big) digits and colors using the specific buttons. 

Check solution

Let the app Check the validity of the solution (see rule 1) by pressing the "Check" button.

 

Rule 1: Within a house (row, box or column) a digit may only occur once

 

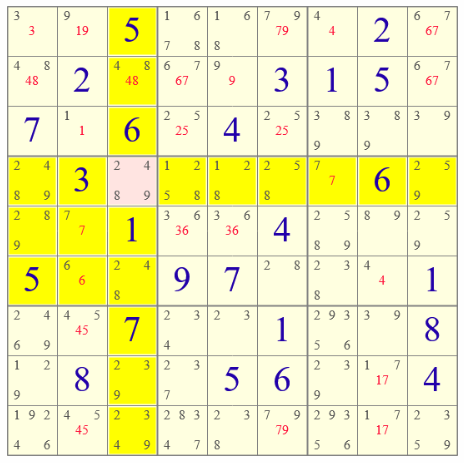
In this sudoko example  cell R4C3 (means row 4, column 3)  contains candidates 2, 4, 8 and 9, marked as corner pencil marks. Column 3 and box 3 already contain a 1, box 4 a 3, column 3 and box 4 a 5, column 3 and row 4 a 6 and column 3 a 7.

So the remaining candidates for R4C3 are determined by aggregating the values of row 4 (36), column 3 (1567) and box 4 (135), together 1, 3, 5, 6 and 7, followed by determining the missing onces. 

Note that a red centred pencil marks are used to emphasize singles, pairs, triples and quadrupes.

 

Rule 2: Locked candidates (pointing and claiming)

 Pointing:

 In this example in box 1 a 6 can only go into row 1, each other 6 in the same row outside box 1 can be eliminated. 

Claiming:

In this example row 2 needs a 6 in R2C7 or R2C9. Therefore value 6 van be eliminated from R1C7.

 

 Rule 3: Naked and hidden singles

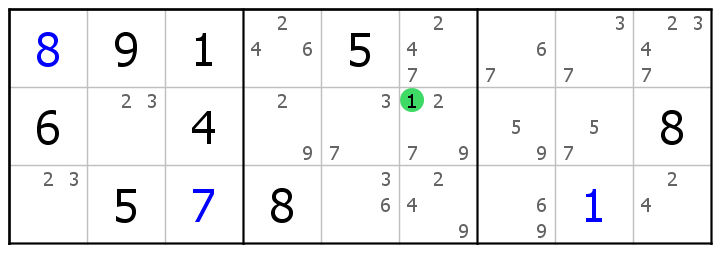
In this example digit 1 in row 2 can only go into R2C6. Therefore all other candidates in R2C6 can be eliminated.

Note that the app doesn't replace the remaining single candidate 1 by a (big) value 1 automatically. This is done when the user presses the "Apply logic" button. Then alle singles are "accepted" by the user. In this way the user can follow the elimination process step by step.

 

Rule 4: Naked and hidden pairs

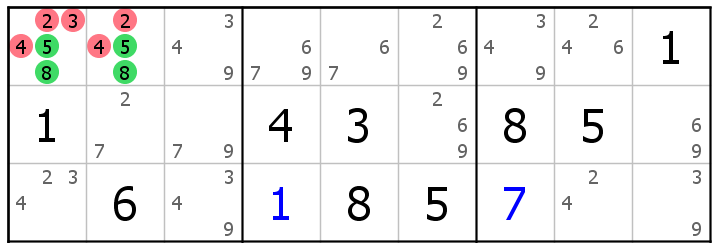
Quite often hidden pairs are difficult to spot. In this example row 1 hides a 58 pair. Therefore the red candidates can be eliminated from R1C12.

 

Rule 5: Naked and hidden triples

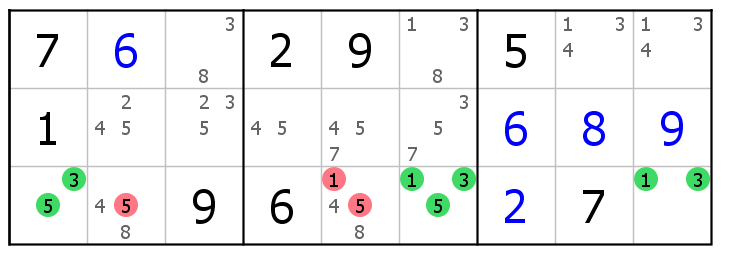
This example shows a naked 135 triple in row 3, 3 candidates for 3 cells.  Candidate 5 can be eliminated from R3C2, candidates 1 and 5 can be eliminated fron R3C5.

 

Rule 6: Naked and hidden quadruples

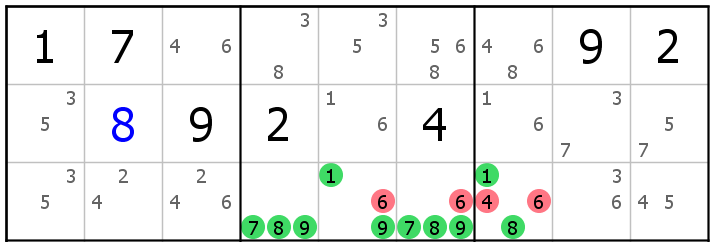
This example shows a hidden 1789 quadruple, 4 candidates for 4 cells. As you see quadruples are very difficult to spot. Here candidate 4 can be eliminated from R3C7 and candidate 6 can be eliminated from R3C567.

Solving techniques

You can find advanced solving techniques here: http://hodoku.sourceforge.net/en/techniques.php

 

Non-functional requirements

Additional requirements:

F Functionality

F001 Import/Load facilities, F002 Usage of colors, F003 Delete functionality

U Useability

U001 Undo/Redo possibility, U002 Reset possibility, U003 Hint/Autosolve possibility, U004 Desktop/Mobile devices

R Reliablility

R001 Autosave possibility, R002 24/7 availability

P Performance

P001  Response within 100ms

S Supportability

S001 Easy adaptable, S002 Easy extendable

 

Analysis and Design

The following table shows basic constructs for process flows, use cases, UML sequence diagrams and source code

  Sequences Selections Loops
Process flow Activities Decisions Repeat loops
Use Case Use case steps Extension points Repeat steps
UML Sequence diagram Operations Option fragments Loop fragments
Source code Instructions Conditions Iterations

 

What you see is that the basic constructs are pretty much the same. Use cases are refinements of processes, (class) operations are refinements of use cases and class operations are transformed to source code.

And that's exactly how the app has been build!

Let's look at the sudoku rule2a (Locked candidates) again.

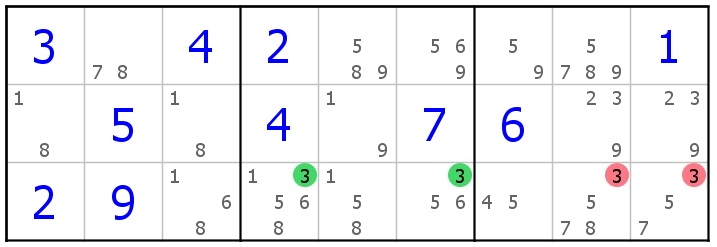
If row 1 in box 1 has a 3 and a 3 can not go to row 2 in box 2, then in row 3 in box 2 the 3's gets locked and the 3's in row 3 in box 3 are eleiminated. The if-statement is a selection and "the 3's in row 3 in box 3 are eliminated" is a sequence. The rule is repeatedin a loop  for 3 clusters of 3 rows in 3 boxes and 3 clusters of 3 columns in 3 boxes.

Also in the way we think we apply sequences, selections and loops. So in fact we can talk here about seamless software development.

 

Let's look at the refinement process for rule 2a: Locked candidates (pointing) again.

Use case step: Apply basic sudoku logic

=>

Requirement refinement:

Apply

  • Rule 1: Within a house (row, box or column) a digit may only occur once
  • Rule 2: Locked candidates (pointing and claiming)
  • Rule 3: Naked and hidden singles
  • Rule 4: Naked and hidden pairs
  • Rule 5: Naked and hidden triples
  • Rule 6: Naked and hidden quadruples

=>

Requirement refinement:

Rule 2: Locked candidates (pointing and claiming)

 Pointing:

 In this example in box 1 a 6 can only go into row 1, each other 6 in the same row outside box 1 can be eliminated. 

=>

Analysis and design:

=>

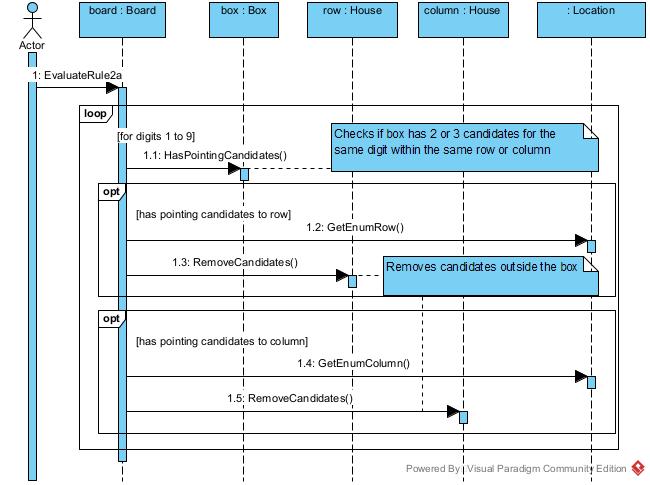
Source code:

    // rule 2a: Locked candidates (pointing)
    Board.prototype._rule2a = function (box) {
        for (var digit = 1; digit <= 9; digit++) {
            var ar = new Array();
            for (var m = 0; m < box.length; m++) {
                var subloc = box[m];
                var cell = this.getCell(subloc);
                if (!cell.isAssigned())
                    if (cell.isAllowed(digit))
                        ar.push(subloc);
            }        
            if (ar.length == 2 || ar.length == 3) {
                // examine array
                //for rows
                var subrow = ar[0].row;
                var isEqual = true;
                for (var n = 1; n < ar.length; n++) {
                    if (ar[n].row !== subrow) {
                        isEqual = false;
                        break;
                    }
                }    
                if (isEqual) {
                    // remove digit from cells in row outside box
                    var rows = ar[0].getSibs(SibType.Row, true);
                    for (var n = 0; n < rows.length; n++) {
                        var found = false;
                        for (var p = 0; p < ar.length; p++) {
                            if (rows[n].col == ar[p].col) {
                                found = true;
                                break;
                            }
                        }
                        if (!found) {
                            var subcell = this.getCell(rows[n]);
                            subcell.removeCandidateCorner(digit);
                        }                    
                    }
                }
                // for columns
                var subcol = ar[0].col;
                var isEqual = true;
                for (var n = 1; n < ar.length; n++) {
                    if (ar[n].col !== subcol) {
                        isEqual = false;
                        break;
                    }
                }    
                if (isEqual) {
                    // remove digit from cells in column outside box
                    var cols = ar[0].getSibs(SibType.Col, true);
                    for (var n = 0; n < cols.length; n++) {
                        var found = false;
                        for (var p = 0; p < ar.length; p++) {
                            if (cols[n].row == ar[p].row) {
                                found = true;
                                break;
                            }
                        }
                        if (!found) {
                            var subcell = this.getCell(cols[n]);
                            subcell.removeCandidateCorner(digit);
                        }                    
                    }
                }
            }
        }    
    }

 

This is how stepwise refinement of requirements works. Dive in the links to get more detail.